Dimensions video series

I just finished watching the challenging Dimensions video series - 9 videos, each 13 minutes long, which teach you how to visualize objects in 4 dimensions. I watched each video as my evening treat for the past week.

Videos 1 and 2 are basic, and you might find parts of them a bit boring. But they're important for the later videos – especially the bit about how rolling a sphere around affects its stereographic projection.



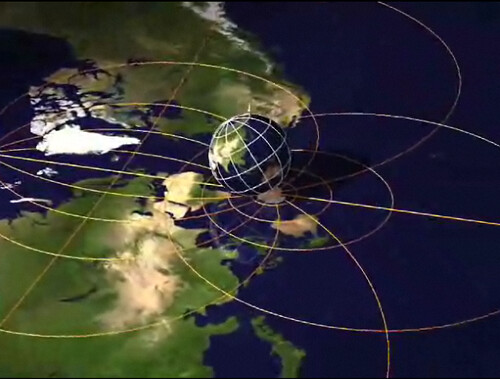
In videos 3 and 4, we start to get into the good stuff: the fourth dimension. For example, if we want to visualize the 4-dimensional equivalent of a cube (called a "hypercube", with 16 nodes and 32 edges), we can get a feel for it by "stereographically projecting" it into 3-dimensions:



Wow!

Next, videos 5 and 6 delve into complex numbers. It was neat to finally get a visual explanation of what the Mandelbrot set represents. It's tricky - it's the set of points for which the Julia set (the blue shape on the right) appears. Outside of the Mandelbrot set, the Julia set disappears.



Video 6 finishes with a beautiful zoom deep into the Mandelbrot set.



Videos 7 and 8 were the most difficult and had me pressing the pause button quite a bit to try to understand what was said. For example, in Video 7 we learn how to divide up a 4-dimensional sphere into circles ("decomposing S3 into its Hopf circles"). Many replays later, I think I get the general idea.



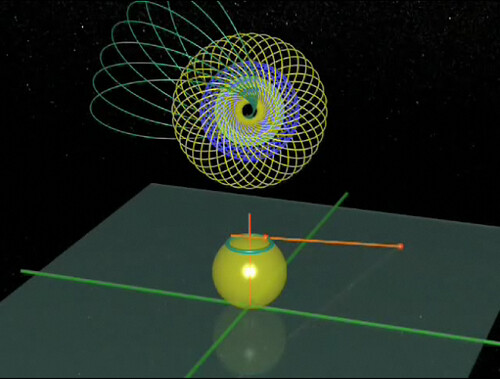
Video 8 almost totally lost me, but I think I get it now. If you highlight a torus (a doughnut shape) in a 4-dimensional sphere (yes, a torus can be a subset of a 4-dimensional sphere) and then stereographically project the torus into 3 dimensions, you get a deformed torus - and it gets REALLY deformed as you roll the sphere around in 4-D land:







These videos have amazing animated visualizations that you'll find nowhere else. And they have a great soundtrack to boot. Go watch!

Stack of books as a First-In-Last-Out stack

My "book stack" is a stack of books that I would like to finish reading someday (or to re-read):



Because of the nature of this stack, books that are frequently used float to the top, and rarely accessed books sink to the bottom.

So at the top is "Teach What You Know" (on training others, which is a part of my job) and "The Pug Handbook" (I'm taking care of my brother's dog this month). Also, "The Art of UNIX Programming", which is a fascinating patterns book recommended by a colleague.

At the bottom are some books I wish I never purchased (note to self: always read a chapter of a book before buying). Why did I spend $50 on "Windows Presentation Foundation"? Good reviews, yes, but I don't use WPF. Again, amazing reviews of "Streamlined Object Modeling", but I have found this text to be rather dry: "R48. [Role] A regular library patron can only collaborate with closed-ended resource holds; a researcher patron can collaborate with open-ended or closed-ended research holds.". Not my style at all.

Great books I've barely started: Programming Pearls. Patterns of Enterprise Application Architecture. And where am I going to find the time to squeeze in Structure and Interpretation of Computer Programs?

Basic Economics is one that I'd like to re-read - it's written in a surprisingly engaging way. I'd also like to re-read Getting Things Done to get a refresher on the fundamentals of that time-management system.

Meaning in the life of a computer programmer

I'm sitting in Seattle airport and, with a few hours to kill, am thinking about how the life of someone who spends most of his time programming computers can have meaning. First, the product that my company is building does help people - it enables them to connect and communicate via social networks. I'm sure that most computer programmers are working on projects that benefit people (whether few or many).

Second, the computer programmer strives with his teammates to solve hard problems. We are yoked together in a struggle against complexity, errors in logic, and legacy code. We assist our neighbor, and in this case our neighbor is our colleagues. Through hard work and professionalism, we love our neighbor and bear each other's crosses.

Bearing one's cross - that is a reality for the computer programmer. There is much that goes wrong, much obtuse legacy code that we wish were otherwise; there is friction, there are problems that are near intractable, and there is not enough time to fix everything we we want to fix. These things teach a person patience, forgiveness, bearing wrongs calmly, hope, gentleness, humility, wisdom, courage, prudence, and fortitude.

I do not need to travel to distant lands to learn these sublime truths. They can be learned in the daily work of a computer programmer.

[Windows Mobile] Haali Reader

I really like Haali Reader. It's a text-file viewer for Pocket PC. The cool thing is that it remembers your last position in the file, for all files. So if you were reading a very long text file in Haali Reader, the next time you open it, you'll start where you left off.

StrengthsFinder personality test ($20)

I just finished taking a 30-minute personality test called StrengthsFinder that identifies your top 5 strengths. The idea is that once you've identified your top strengths, you will profit more by working on your strengths rather than on your weaknesses. Interesting idea.

So when you interact with me, here are some traits that you can expect:

• Harmony. Our conversation will be pleasant and productive. Even if we hold different views, we can build on common ground. Rather than spending energy on debate and confrontation, we'll discuss practical matters and get things done.


• Consistency. I treat all people with dignity and avoid any kind of favoritism, bigotry, and dishonesty. If I agree to do something for you, I will keep my word. I create checklists, procedures, and systems to make sure that I don't forget to do things.


• Maximizer. I can take something great and improve it to be even greater. Hand me good work, and I'll make it even better. Hand me shoddy work and I will be grumpy. I also have a knack for noticing the strengths in other people.

If you want to take the test, you'll need to buy the $20 book "StrengthsFinder 2.0". It has a one-time-use code in the back that you can use to access the StrengthsFinder website.

Screenshot of one of the questions:

Aeron chair User Group

I have created an Aeron User Group site, for people who use the Aeron chair manufactured by Herman Miller.

Fairly good chair – looks nice; not sure if it's any more comfortable than a standard upholstered chair.

Also I've been reading a book called "Pain Free at Your PC" that says there's no need to "sit in a specially designed chair". Instead, the key to preventing wrist pain is, surprisingly, good spinal posture:

Pull your head and shoulders back as far as you can. Feel the S-curve develop its arch in your lower back?...You should see that now there is a space under the wrist immediately behind the palm of your hand.

That was a neat discovery. I have discarded my rolled-up towel and SmartGloves – sitting up straight elevates my wrists in the same way.